Zadanie nr 3506892
Wiadomo, że wielomian 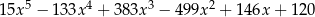 ma w zbiorze
ma w zbiorze 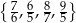 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A) 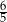 B)
B)  C)
C) 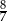 D)
D) 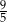
Rozwiązanie
Na mocy twierdzenia o wymiernych pierwiastkach wielomianu, jeżeli ułamek nieskracalny 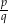 jest pierwiastkiem danego wielomianu, to
jest pierwiastkiem danego wielomianu, to 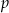 jest dzielnikiem
jest dzielnikiem
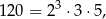
a 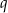 jest dzielnikiem
jest dzielnikiem
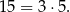
Wśród podanych ułamków tylko 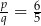 spełnia te dwa warunki.
spełnia te dwa warunki.
Odpowiedź: A

