Zadanie nr 3646454
Liczba 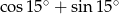 jest równa
jest równa
A) 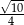 B)
B) 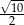 C)
C) 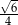 D)
D) 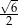
Rozwiązanie
Sposób I
Korzystamy ze wzorów
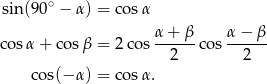
Mamy zatem
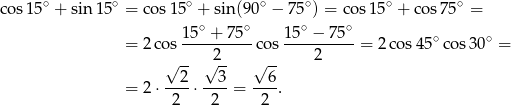
Sposób II
Korzystamy ze wzorów
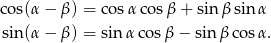
Mamy więc
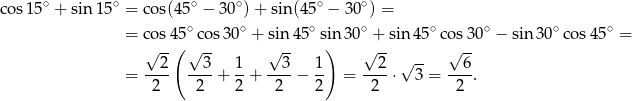
Sposób III
Tym razem użyjemy jedynki trygonometrycznej i wzoru
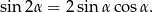
Mamy więc
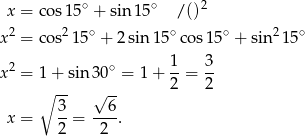
Odpowiedź: D

