Zadanie nr 3750621
Punkt 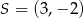 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 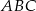 . Prosta zawierająca bok
. Prosta zawierająca bok 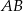 tego trójkąta ma równanie
tego trójkąta ma równanie 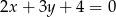 . Prosta zawierająca bok
. Prosta zawierająca bok 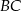 może mieć równanie
może mieć równanie
A) 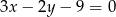 B)
B) 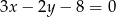 C)
C) 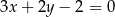 D)
D) 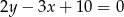
Rozwiązanie
Środek okręgu wpisanego w trójkąt 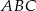 jest równo odległy od wszystkich boków trójkąta, więc odległość punktu
jest równo odległy od wszystkich boków trójkąta, więc odległość punktu 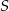 od prostych
od prostych 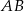 i
i 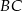 musi być taka sama. Korzystamy ze wzoru na odległość punktu
musi być taka sama. Korzystamy ze wzoru na odległość punktu 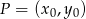 od prostej
od prostej 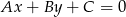 :
:
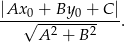
Odległość punktu 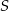 od prostej
od prostej 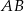 jest więc równa
jest więc równa
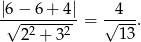
Sprawdzamy teraz, dla której z podanych prostych odległość od punktu 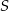 też jest równa
też jest równa 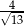 . Łatwo sprawdzić, że tak jest tylko w przypadku prostej:
. Łatwo sprawdzić, że tak jest tylko w przypadku prostej: 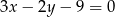 .
.
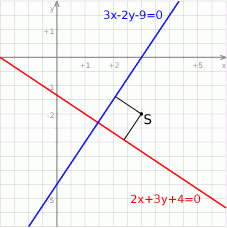
Odpowiedź: A

