Zadanie nr 3766047
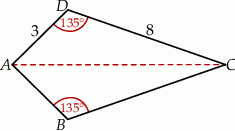
Czworokąt 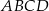 jest deltoidem (zobacz rysunek), w którym
jest deltoidem (zobacz rysunek), w którym 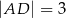 ,
, 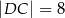 oraz
oraz 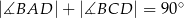 .
.
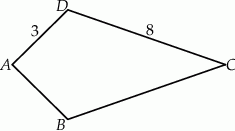
Pole tego deltoidu jest równe
A) 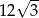 B)
B) 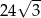 C)
C) 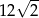 D)
D) 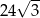
Rozwiązanie
Przekątna 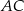 deltoidu jest jego osią symetrii, więc trójkąty
deltoidu jest jego osią symetrii, więc trójkąty 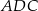 i
i 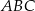 są przystające.
są przystające.
W szczególności
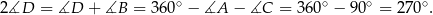
Zatem
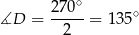
oraz
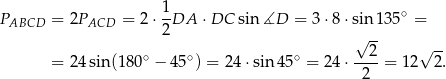
Odpowiedź: C

