Zadanie nr 3770292
Zbiorem wartości funkcji 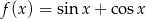 , gdzie
, gdzie 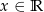 , jest przedział
, jest przedział
A) 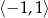 B)
B) 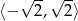 C)
C) 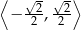 D)
D) 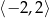
Rozwiązanie
Sposób I
Korzystamy ze wzoru na sinus sumy
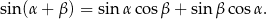
Mamy zatem
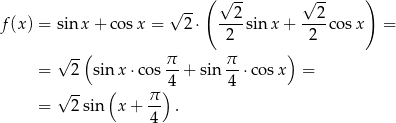
Ponieważ
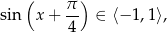
zbiorem wartości funkcji 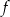 jest przedział
jest przedział
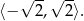
Sposób II
Korzystamy ze wzorów
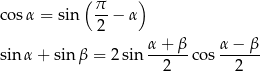
Mamy zatem
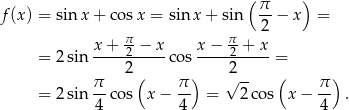
Zbiorem wartości funkcji 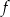 jest więc przedział
jest więc przedział
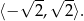
Odpowiedź: B

