/Szkoła średnia/Zadania testowe

Zadanie nr 3921289

Dodaj do ulubionych
Dodaj do rozwiązanych

Ciągiem rosnącym jest ciąg o wyrazie ogólnym
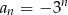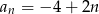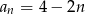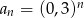
A) an = − 3n B) an = − 4 + 2n C) an = 4 − 2n D) an = (0,3)n

Rozwiązanie

Sposób I

Wypisujemy (lub liczymy w pamięci) pierwsze dwa wyrazy każdego z ciągów. Gdy się to zrobi, okaże się, że rosnący może być tylko ciąg 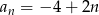an = − 4 + 2n .

Sposób II

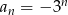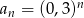Ciągi a = − 3n n i a = (0,3)n n są geometryczne z ilorazem mniejszym od 1, więc nie są rosnące.
Ciąg 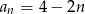an = 4− 2n jest arytmetyczny z ujemną różnicą, więc jest malejący.
Ciąg 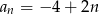an = − 4+ 2n jest arytmetyczny z dodatnią różnicą, więc jest rosnący.

Sposób III

Liczymy

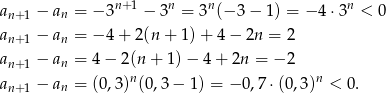
an+1 − an = − 3n+ 1 − 3n = 3n(− 3 − 1) = − 4 ⋅3n < 0 a − a = − 4 + 2(n + 1) + 4 − 2n = 2 n+1 n an+1 − an = 4 − 2(n + 1 )− 4 + 2n = − 2 a − a = (0,3)n(0 ,3− 1 ) = − 0,7⋅ (0,3)n < 0. n+1 n

Widać, że rosnący jest ciąg 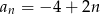an = − 4+ 2n .  
Odpowiedź: B

Wersja PDF