/Szkoła średnia/Zadania testowe

Zadanie nr 4028038

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile jest liczb całkowitych spełniających nierówność 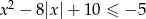2 x − 8|x|+ 10 ≤ − 5 ?
A) 1 B) 2 C) 3 D) 6

Rozwiązanie

Zapiszmy daną nierówność w postaci

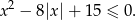
2 x − 8|x |+ 15 ≤ 0.

Sposób I

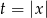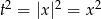Jeżeli podstawimy t = |x| , to 2 2 2 t = |x | = x , więc daną nierówność możemy zapisać w postaci

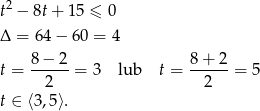
2 t − 8t+ 1 5 ≤ 0 Δ = 64 − 60 = 4 8 − 2 8 + 2 t = ------= 3 lub t = ------= 5 2 2 t ∈ ⟨3,5⟩.

Mamy zatem

3 ≤ |x| ≤ 5.

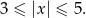
Jest 6 liczb całkowitych spełniających ten warunek

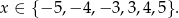
x ∈ {− 5,− 4,− 3,3,4,5} .

Sposób II

Jeżeli lewą stronę nierówności zapiszemy w postaci

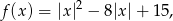
2 f(x ) = |x| − 8|x| + 15,

to wykres funkcji 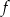f otrzymujemy z wykresu funkcji

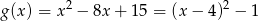
2 2 g (x) = x − 8x + 15 = (x− 4) − 1

przez odbicie części wykresu znajdującej się na prawo od osi 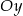Oy względem osi 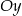Oy . Szkicujemy ten wykres.

PIC

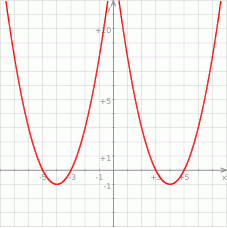
Z wykresu widać, że jest 6 liczb całkowitych spełniających nierówność 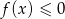f (x) ≤ 0

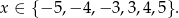
x ∈ {− 5,− 4,− 3,3,4,5} .

 
Odpowiedź: D

Wersja PDF