Zadanie nr 4126519
Dany jest trójkąt 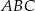 , w którym
, w którym 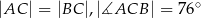 , zaś
, zaś 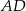 jest dwusieczną kąta
jest dwusieczną kąta 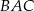 i
i 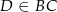 . Wówczas miara kąta
. Wówczas miara kąta 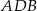 jest równa
jest równa
A) 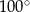 B)
B) 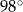 C)
C) 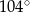 D)
D) 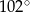
Rozwiązanie
Zaczynamy od rysunku
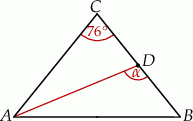
Trójkąt  jest trójkątem równoramiennym, więc kąt
jest trójkątem równoramiennym, więc kąt 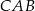 jest równy kątowi
jest równy kątowi 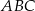 . Zatem
. Zatem
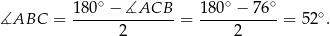
Odcinek 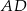 jest dwusieczną kąta
jest dwusieczną kąta 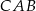 , więc
, więc
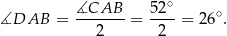
Teraz już łatwo obliczyć szukany kąt
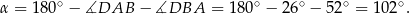
Odpowiedź: D

