/Szkoła średnia/Zadania testowe

Zadanie nr 4173267

Dodaj do ulubionych
Dodaj do rozwiązanych

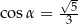Kąt α jest ostry i √5- cosα = 3 . Wobec tego
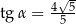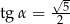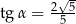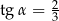
A) √ - tg α = 4-5- 5 B) √- tg α = -5- 2 C) 2√ 5 tg α = --5- D) 2 tgα = 3

Rozwiązanie

Sposób I

Narysujmy trójkąt prostokątny, w którym 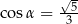√ - cosα = -35 .

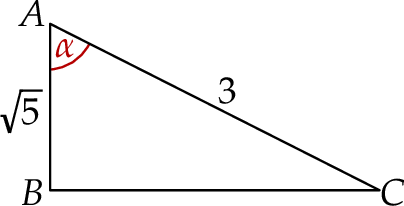
ZINFO-FIGURE

Na mocy twierdzenia Pitagorasa mamy

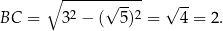
∘ ------√---- √ -- BC = 32 − ( 5)2 = 4 = 2.

Stąd

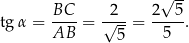
BC 2 2√ 5- tgα = ----= √---= ----. AB 5 5

Sposób II

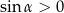Ponieważ α jest kątem ostrym, więc sinα > 0 . Zatem z jedynki trygonometrycznej otrzymujemy

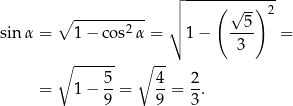
┌│ ----(-----)-- ∘ ---------- │ √ 5- 2 sin α = 1 − cos2α = ∘ 1 − ---- = 3 ∘ ------ ∘ -- = 1 − 5-= 4-= 2. 9 9 3

Liczymy wartość tangensa

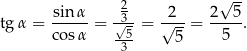
√ -- sin α 23 2 2 5 tgα = ----- = √5-= √---= ----. cos α -3- 5 5

 
Odpowiedź: C

Wersja PDF