/Szkoła średnia/Zadania testowe

Zadanie nr 4248946

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy długości 80 cm i krawędzi bocznej długości 90 cm (zobacz rysunek), a ponadto dane są cztery odcinki 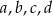a,b,c,d , o długościach – odpowiednio – 53 cm, 59 cm, 63 cm i 69 cm.

PIC

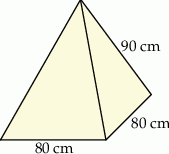
Wysokość tego ostrosłupa jest dłuższa
A) tylko od odcinka a .
B) tylko od odcinków a i b .
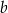C) tylko od odcinków 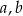a,b i c .
D) od wszystkich czterech danych odcinków.

Rozwiązanie

Dorysujmy wysokość, o której mowa w treści zadania.

PIC

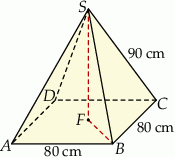
Korzystamy z twierdzenia Pitagorasa w trójkącie 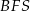BF S .

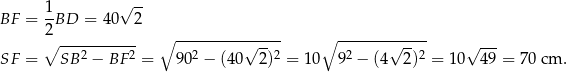
√ -- BF = 1-BD = 40 2 2 ∘ --------------- ∘ ------------- ∘ ---2------2 2 √ --2 2 √ -- 2 √ --- SF = SB − BF = 90 − (40 2) = 10 9 − (4 2 ) = 10 49 = 70 cm .

Wysokość jest więc dłuższa od wszystkich czterech odcinków.  
Odpowiedź: D

Wersja PDF