Zadanie nr 4453850
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe
A) 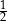 B)
B) 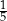 C)
C)  D)
D) 
Rozwiązanie
Jeżeli za zdarzenia elementarne przyjmiemy pary otrzymanych liczb oczek to
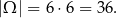
Sposób I
Wypiszmy zdarzenia sprzyjające
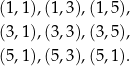
Interesujące nas prawdopodobieństwo jest więc równe
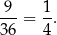
Sposób II
Jeżeli iloczyn liczb wyrzuconych oczek jest nieparzysty, to obie wyrzucone liczby muszą być nieparzyste. Jest więc
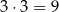
takich zdarzeń. Interesujące nas prawdopodobieństwo jest więc równe
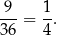
Odpowiedź: C

