/Szkoła średnia/Zadania testowe

Zadanie nr 4554961

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole pierścienia kołowego na rysunku jest równe 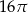1 6π (mniejszy okrąg jest styczny do boków kwadratu 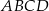ABCD , a do większego okręgu należą punkty 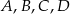A ,B,C ,D ). Zatem długość boku kwadratu 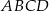ABCD jest równa:

PIC

A) 2 B) 4 C) 8 D) 16

Rozwiązanie

Oznaczmy przez 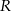R i r promienie odpowiednio większego i mniejszego okręgu, a przez a długość boku kwadratu.

PIC

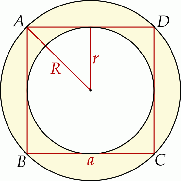
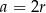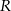Bok kwadratu jest równy a = 2r , a R jest połową długości przekątnej, czyli

√ -- a--2- R = 2

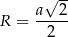
Z podanego pola pierścienia mamy

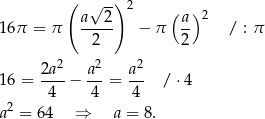
( -) a√ 2 2 ( a) 2 16π = π ----- − π -- / : π 2 2 2 2 2 16 = 2a--− a--= a-- / ⋅4 4 4 4 a2 = 64 ⇒ a = 8.

 
Odpowiedź: C

Wersja PDF