Zadanie nr 4615474
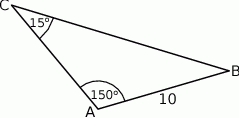
Pole trójkąta przedstawionego na rysunku jest równe
A) 50 B) 25 C) 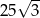 D)
D) 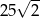
Rozwiązanie
Trzeci kąt trójkąta ma miarę
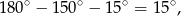
więc dany trójkąt jest równoramienny i 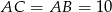 . Liczymy pole trójkąta korzystając ze wzoru z sinusem
. Liczymy pole trójkąta korzystając ze wzoru z sinusem
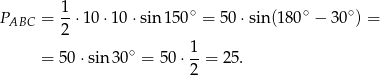
Odpowiedź: B

