/Szkoła średnia/Zadania testowe

Zadanie nr 4619471

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile rozwiązań ma układ równań 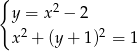{ 2 y = x − 2 x2 + (y + 1)2 = 1 ?
A) 0 B) 1 C) 2 D) 3

Rozwiązanie

Sposób I

Szkicujemy zbiory opisane równaniami układu. Pierwsze równanie to parabola 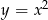2 y = x przesunięta o 2 jednostki w dół, a drugie to okrąg o środku 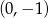(0,− 1) i promieniu √ -- 2 ≈ 1,4 .

PIC

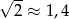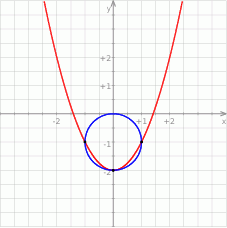
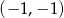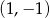Jeżeli wykonamy rysunek wystarczająco dokładnie (np. zauważając, że punkty (− 1,− 1) i (1,− 1) leżą na paraboli), to widać, że parabola i okrąg przecinają się w 3 punktach.

Sposób II

Sprawdzamy liczbę rozwiązań algebraicznie. Podstawiamy 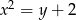2 x = y + 2 z pierwszego równania do drugiego.

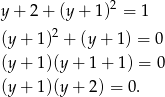
y+ 2+ (y+ 1)2 = 1 2 (y+ 1) + (y+ 1) = 0 (y+ 1)(y+ 1+ 1) = 0 (y+ 1)(y+ 2) = 0.

Dla 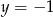y = − 1 otrzymujemy dwa punkty wspólne, bo wtedy 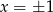x = ± 1 , a dla 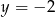y = − 2 jest jeden punkt przecięcia, bo wtedy x = 0 .  
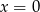Odpowiedź: D

Wersja PDF