/Szkoła średnia/Zadania testowe

Zadanie nr 4706461

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile rozwiązań ma układ równań 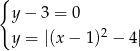{ y − 3 = 0 y = |(x − 1)2 − 4|
A) 1 B) 2 C) 3 D) 4

Rozwiązanie

Sposób I

Podstawiamy 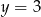y = 3 z pierwszego równania do drugiego i mamy

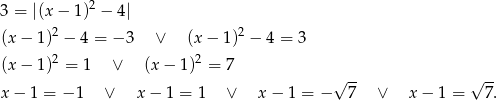
2 3 = |(x − 1) − 4| (x − 1)2 − 4 = − 3 ∨ (x − 1 )2 − 4 = 3 2 2 (x − 1) = 1 ∨ (x− 1) = 7 x − 1 = − 1 ∨ x− 1 = 1 ∨ x − 1 = −√ 7- ∨ x− 1 = √ 7.

Widać zatem, że układ ma cztery rozwiązania.

Sposób II

Szkicujemy rozwiązania obu równań w układzie współrzędnych. Pierwsze równanie układu to pozioma prosta 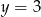y = 3 , a wykres drugiego równania otrzymamy przesuwając parabolę 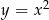y = x2 o jedną jednostkę w prawo i cztery w dół, a następnie odbijając część poniżej osi 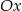Ox do góry.

PIC

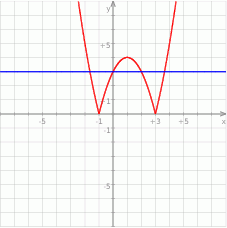
Gdy zrobimy rysunek widać, że dwa wykresy mają cztery punkty wspólne.  
Odpowiedź: D

Wersja PDF