Zadanie nr 4754589
Proste o równaniach 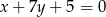 i
i 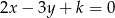 przecinają się na osi
przecinają się na osi 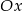 . Zatem parametr
. Zatem parametr 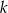 jest równy
jest równy
A) 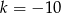 B)
B) 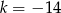 C)
C) 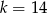 D)
D) 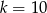
Rozwiązanie
Sposób I
Wyznaczmy punkt przecięcia prostej 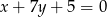 z osią
z osią 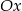 (podstawiamy
(podstawiamy 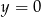 ).
).
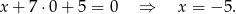
W tym samym punkcie druga prosta ma przecinać oś 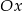 , więc musi być
, więc musi być
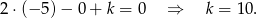
Sposób II
Wyznaczmy punkt wspólny danych prostych
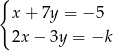
Odejmujemy od drugiego równania pierwsze pomnożone przez 2 (żeby skrócić  ) i mamy
) i mamy
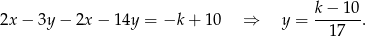
Jeżeli punkt wspólny ma leżeć na osi 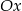 , to musi być
, to musi być 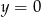 , czyli
, czyli 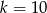 .
.
Odpowiedź: D

