Zadanie nr 4952725
Dany jest ciąg arytmetyczny 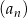 określony wzorem
określony wzorem 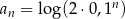 dla każdej liczby naturalnej
dla każdej liczby naturalnej 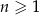 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 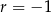 B)
B) 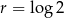 C)
C) 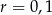 D)
D) 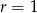
Rozwiązanie
Sposób I
Ponieważ
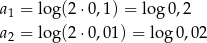
to
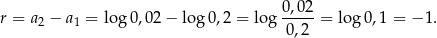
Sposób II
Zauważmy, że
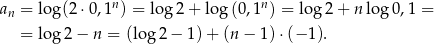
To oznacza, że jest to ciąg arytmetyczny o różnicy 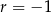 .
.
Odpowiedź: A

