Zadanie nr 5283153
W równoległoboku 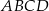 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 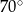 .
.
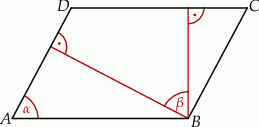
Wtedy kąt 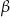 ma miarę
ma miarę
A) 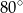 B)
B) 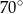 C)
C) 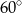 D)
D) 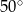
Rozwiązanie
Oznaczmy przez 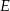 i
i 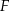 zaznaczone na rysunku rzuty punktu
zaznaczone na rysunku rzuty punktu 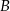 na proste
na proste 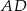 i
i 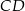 odpowiednio.
odpowiednio.
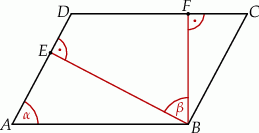
Sposób I
Zauważmy, że łatwo możemy obliczyć miarę kąta przy wierzchołku 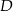 czworokąta
czworokąta 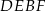
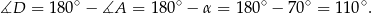
Suma kątów w czworokącie 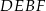 jest równa
jest równa 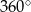 , więc
, więc

Sposób II
Tym razem popatrzmy na trójkąty prostokątne 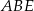 i
i 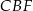 .
.
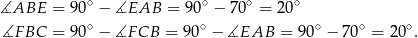
Stąd
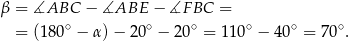
Odpowiedź: B

