Zadanie nr 5290766
Wszystkie wyrazy rosnącego ciągu arytmetycznego 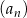 , gdzie
, gdzie 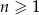 są dodatnimi liczbami całkowitymi. Jeżeli
są dodatnimi liczbami całkowitymi. Jeżeli 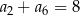 , to suma dziesięciu początkowych wyrazów ciągu
, to suma dziesięciu początkowych wyrazów ciągu 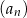 jest równa
jest równa
A) 45 B) 66 C) 55 D) 48
Rozwiązanie
Wiemy, że
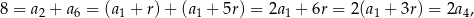
czyli 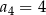 . Wiemy jednak dodatkowo, że ciąg
. Wiemy jednak dodatkowo, że ciąg 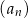 jest rosnący i że wszystkie jego wyrazy są dodatnimi liczbami całkowitymi – to nie zostawia zbyt dużego wyboru na wartości wyrazów
jest rosnący i że wszystkie jego wyrazy są dodatnimi liczbami całkowitymi – to nie zostawia zbyt dużego wyboru na wartości wyrazów 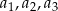 . Jedyna możliwość, to
. Jedyna możliwość, to
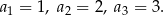
Mamy zatem
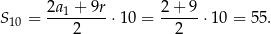
Odpowiedź: C

