Zadanie nr 5298162
Największa wartość funkcji 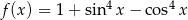 określonej dla
określonej dla 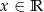 to
to
A) 1 B) 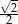 C)
C) 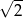 D) 2
D) 2
Rozwiązanie
Korzystamy ze wzoru
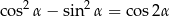
Mamy zatem
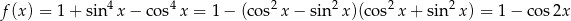
Widać teraz, że największą wartość funkcji 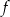 otrzymamy, gdy
otrzymamy, gdy 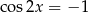 , czyli np. dla
, czyli np. dla 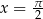
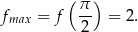
Odpowiedź: D
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Największa wartość funkcji 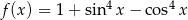 określonej dla
określonej dla 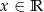 to
to
A) 1 B) 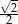 C)
C) 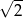 D) 2
D) 2
Korzystamy ze wzoru
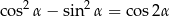
Mamy zatem
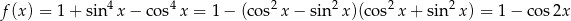
Widać teraz, że największą wartość funkcji 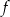 otrzymamy, gdy
otrzymamy, gdy 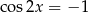 , czyli np. dla
, czyli np. dla 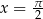
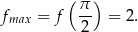
Odpowiedź: D
