Zadanie nr 5310024
Punkt 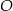 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
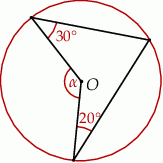
A) 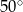 B)
B) 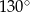 C)
C) 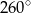 D)
D) 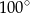
Rozwiązanie
Dorysujmy promień 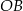 okręgu.
okręgu.
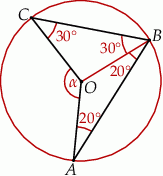
Zauważmy, że trójkąty 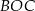 i
i 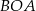 są równoramienne, więc
są równoramienne, więc
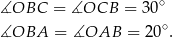
Sposób I
Korzystamy z zależności między kątami środkowym i wpisanym opartymi na tym samym łuku.
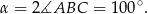
Sposób II
Z trójkątów równoramiennych 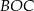 i
i 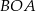 mamy
mamy
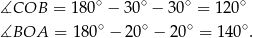
Zatem
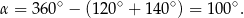
Odpowiedź: D

