Zadanie nr 5655789
Wysokość graniastosłupa prawidłowego trójkątnego jest równa połowie długości jego krawędzi podstawy. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
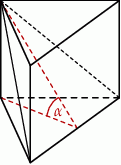
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 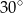 B)
B) 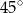 C)
C) 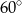 D)
D) 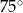
Rozwiązanie
Oznaczmy wysokość graniastosłupa przez 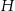 , a wysokość trójkąta w podstawie przez
, a wysokość trójkąta w podstawie przez 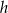 .
.
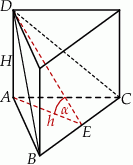
Z założenia bok trójkąta w podstawie graniastosłupa ma długość 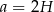 , więc
, więc
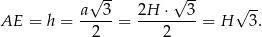
Stąd
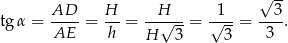
To oznacza, że 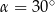 .
.
Odpowiedź: A

