/Szkoła średnia/Zadania testowe

Zadanie nr 5991300

Dodaj do ulubionych
Dodaj do rozwiązanych

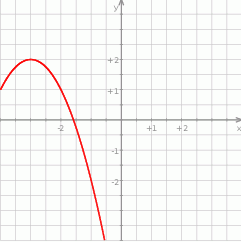
W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie 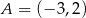A = (− 3,2) , która jest wykresem funkcji kwadratowej f .

PIC

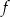Funkcja 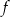f może być opisana wzorem
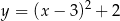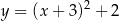
A) y = (x − 3)2 + 2 B) y = (x + 3)2 + 2
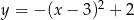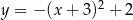
C) 2 y = − (x − 3) + 2 D) 2 y = − (x + 3) + 2

Rozwiązanie

Sposób I

Korzystając z postaci kanonicznej funkcji kwadratowej oraz z podanej informacji o wierzchołku 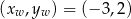(xw ,yw ) = (− 3,2) mamy

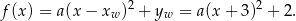
f(x) = a(x − xw )2 + yw = a(x+ 3)2 + 2.

Z wykresu widać ponadto, że ramiona paraboli są skierowane w dół, więc 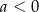a < 0 . Wśród podanych wzorów tylko 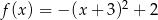f(x) = − (x + 3 )2 + 2 ma tę postać.

Sposób II

Z wykresu widać, że szukana funkcja 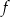f spełnia warunek 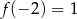f(− 2) = 1 . Sprawdzając podane wzory łatwo zauważyć, że tylko funkcja 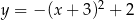y = − (x + 3)2 + 2 ma tę własność.  
Odpowiedź: D

Wersja PDF