Zadanie nr 6081564
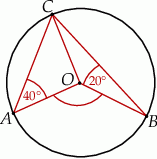
Punkty 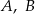 i
i 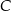 leżą na okręgu o środku
leżą na okręgu o środku 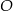 (zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy
(zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy 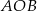 ma miarę
ma miarę
A) 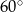 B)
B) 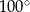 C)
C) 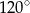 D)
D) 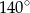
Rozwiązanie
Zauważmy, że każdy z trójkątów 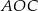 i
i 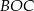 jest równoramienny.
jest równoramienny.
Sposób I
Liczymy
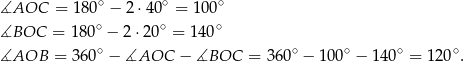
Sposób II
Korzystając z twierdzenia o kątach wpisanym i środkowym mamy
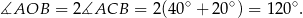
Odpowiedź: C

