Zadanie nr 6115220
O funkcji liniowej 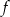 wiadomo, że
wiadomo, że 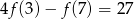 i
i 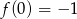 . Zatem
. Zatem
A) 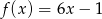 B)
B) 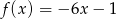 C)
C) 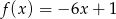 D)
D) 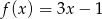
Rozwiązanie
Sposób I
Sprawdzamy, która z podanych funkcji spełnia żądane warunki. Gdy to zrobimy, okaże się, że jest to funkcja 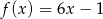 .
.
Sposób II
Szukamy funkcji 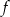 w postaci
w postaci 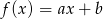 . Warunek
. Warunek 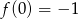 oznacza, że
oznacza, że 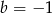 . Rozpisujemy drugi z podanych warunków.
. Rozpisujemy drugi z podanych warunków.
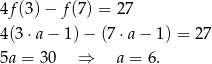
Zatem funkcja 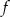 jest dana wzorem
jest dana wzorem
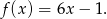
Odpowiedź: A

