Zadanie nr 6203799
Układ równań 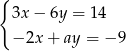 opisuje w układzie współrzędnych zbiór pusty dla
opisuje w układzie współrzędnych zbiór pusty dla
A) 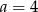 B)
B) 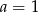 C)
C) 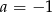 D)
D) 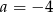
Rozwiązanie
Sposób I
Dodajmy do drugiego równania pierwsze pomnożone przez  (żeby skrócić
(żeby skrócić  ) i mamy
) i mamy
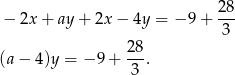
Widać teraz, że układ jest sprzeczny tylko dla 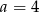 .
.
Sposób II
Jeżeli układ ma być sprzeczny, to jego równania muszą opisywać dwie różne proste równoległe. Ponieważ 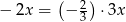 , to musimy też mieć
, to musimy też mieć
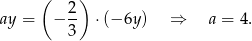
Odpowiedź: A

