Zadanie nr 6503883
W każdym z pięciu pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 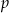 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
A) 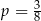 B)
B) 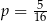 C)
C) 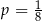 D)
D) 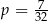
Rozwiązanie
Kulę z każdego z pojemników możemy wybrać na dwa sposoby, więc pięć kul możemy wybrać na
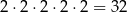
sposoby.
Sposób I
Zdarzeń sprzyjających jest 10:
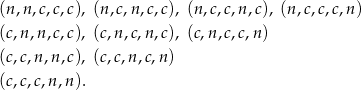
Prawdopodobieństwo jest więc równe
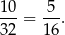
Sposób II
Zdarzeń sprzyjających jest
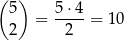
(wybieramy dwa miejsca dla niebieskich kul). Prawdopodobieństwo jest więc równe
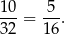
Odpowiedź: B

