Zadanie nr 6990761
Dany jest ciąg geometryczny 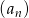 , określony dla
, określony dla 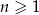 , w którym
, w którym 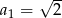 ,
, 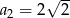 ,
, 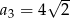 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 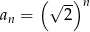 B)
B) 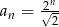 C)
C) 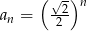 D)
D) 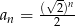
Rozwiązanie
Liczymy iloraz ciągu
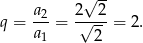
Zatem ciąg ma wzór
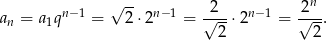
Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest ciąg geometryczny 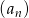 , określony dla
, określony dla 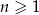 , w którym
, w którym 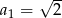 ,
, 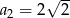 ,
, 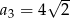 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 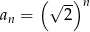 B)
B) 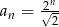 C)
C) 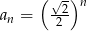 D)
D) 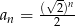
Liczymy iloraz ciągu
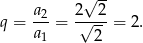
Zatem ciąg ma wzór
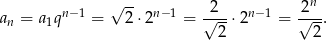
Odpowiedź: B
