Zadanie nr 7013109
Na rysunku przedstawiony jest fragment prostej o równaniu 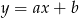 przechodzącej przez punkty
przechodzącej przez punkty 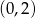 i
i 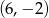 .
.
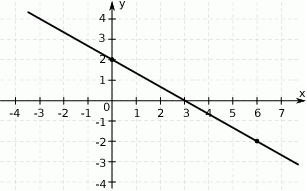
Wtedy
A) 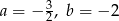 B)
B) 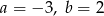 C)
C) 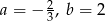 D)
D) 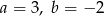
Rozwiązanie
Współczynnik 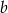 jest równy drugiej współrzędnej punktu wspólnego danej prostej i osi
jest równy drugiej współrzędnej punktu wspólnego danej prostej i osi 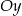 , więc
, więc 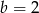 .
.
Sposób I
Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 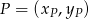 i
i 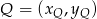 :
:
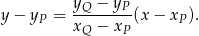
Współczynnik kierunkowy  jest więc równy
jest więc równy
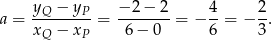
Sposób II
Podstawiając współrzędne danych punktów do równania prostej otrzymujemy układ równań
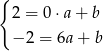
Z pierwszego równania mamy 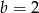 , a z drugiego
, a z drugiego
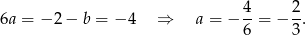
Odpowiedź: C

