Zadanie nr 7309842
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była biała. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z drugiej z tych urn, jest równe
A) 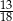 B)
B) 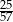 C)
C) 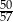 D)
D) 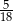
Rozwiązanie
Niech 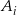 ,
, 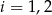 oznacza zdarzenie polegające na wylosowaniu urny o numerze
oznacza zdarzenie polegające na wylosowaniu urny o numerze 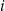 , a
, a 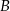 oznacza zdarzenie polegające na wyborze białej kuli. Musimy więc obliczyć
oznacza zdarzenie polegające na wyborze białej kuli. Musimy więc obliczyć
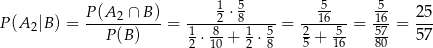
Odpowiedź: B

