Zadanie nr 7573239
Losujemy jedną liczbę czterocyfrową. Prawdopodobieństwo 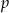 otrzymania liczby, której cyfry to 1,1,2,2 (w dowolnej kolejności) spełnia warunek
otrzymania liczby, której cyfry to 1,1,2,2 (w dowolnej kolejności) spełnia warunek
A) 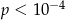 B)
B) 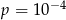 C)
C) 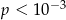 D)
D) 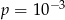
Rozwiązanie
Wszystkich liczb czterocyfrowych jest
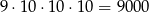
(można też liczyć tak: 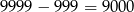 ).
).
Liczb o cyfrach 1,1,2,2 jest 6:
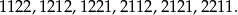
Zatem prawdopodobieństwo wynosi
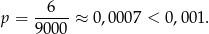
Odpowiedź: C

