Zadanie nr 8084214
Kąt między ramionami trójkąta równoramiennego ma miarę 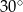 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 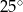 B)
B) 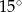 C)
C) 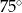 D)
D) 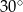
Rozwiązanie
Zaczynamy od szkicowego rysunku.
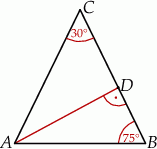
Ponieważ suma kątów w trójkącie jest równa 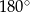 , to suma dwóch kątów w podstawie trójkąta musi być równa
, to suma dwóch kątów w podstawie trójkąta musi być równa
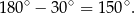
Ponieważ jednak oba te kąty mają tę samą miarę, każdy z nich musi mieć miarę 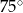 . Zatem interesujący nas kąt ma miarę (patrzymy na sumę kątów w trójkącie
. Zatem interesujący nas kąt ma miarę (patrzymy na sumę kątów w trójkącie 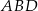 )
)
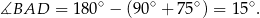
Odpowiedź: B

