/Szkoła średnia/Zadania testowe

Zadanie nr 8132227

Dodaj do ulubionych
Dodaj do rozwiązanych

Symetralna odcinka 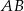AB , gdzie 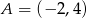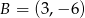A = (− 2,4) , B = (3,− 6) ma równanie
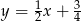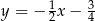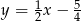A) y = 12x + 34 B) y = − 12x − 34 C) y = 1x− 5 2 4 D) y = 2x − 2

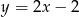
Rozwiązanie

Zaczynamy od rysunku

PIC

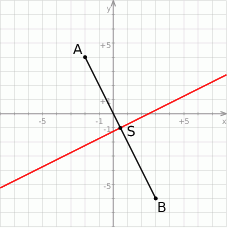
Wyznaczamy równanie prostej 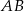AB – szukamy prostej w postaci 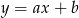y = ax + b i podstawiamy współrzędne punktów 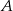A i B .

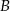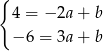
{ 4 = − 2a + b − 6 = 3a + b

Odejmujemy od drugiego równania pierwsze i mamy

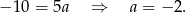
− 10 = 5a ⇒ a = − 2.

Sposób I

Symetralna musi być prostopadła do prostej 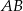AB , czyli musi być postaci 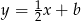y = 12x + b . Jest tylko jedna odpowiedź tej postaci.

Sposób II

Obliczamy współrzędną środka odcinka 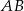AB .

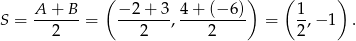
( ) ( ) A--+-B- −-2+--3 4-+-(−-6) 1- S = 2 = 2 , 2 = 2 ,− 1 .

Symetralna jest prostopadła do prostej 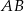AB , więc ma równanie postaci 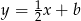1 y = 2x + b . Współczynnik 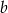b obliczmy podstawiając współrzędne punktu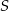 S

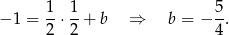
− 1 = 1-⋅ 1-+ b ⇒ b = − 5. 2 2 4

Symetralna ma więc równanie 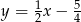1 5 y = 2x− 4 .

Sposób III

Symetralna odcinka 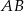AB to zbiór punktów 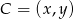C = (x ,y) , dla których

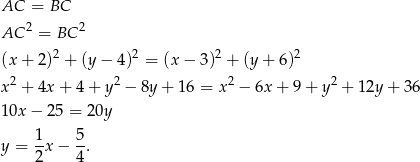
AC = BC 2 2 AC = BC (x + 2)2 + (y − 4)2 = (x − 3 )2 + (y + 6)2 x 2 + 4x + 4 + y 2 − 8y + 16 = x2 − 6x + 9 + y2 + 12y + 3 6 10x − 25 = 20y 1- 5- y = 2x − 4.

 
Odpowiedź: C

Wersja PDF