/Szkoła średnia/Zadania testowe

Zadanie nr 8728705

Dodaj do ulubionych
Dodaj do rozwiązanych

W pewnej szkole liczącej 400 uczniów 83% uczy się języka angielskiego, 51% – języka rosyjskiego, a 42% uczy się obu tych języków. Wynika stąd, że liczba uczniów, którzy nie uczą się żadnego z tych języków, to
A) 56 B) 48 C) 168 D) 32

Rozwiązanie

Sposób I

Zauważmy, że 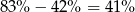83% − 42% = 41% uczniów uczy się tylko języka angielskiego, więc

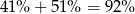
41% + 51% = 92%

uczniów uczy się przynajmniej jednego języka. W takim razie liczba uczniów, którzy nie uczą się żadnego języka jest równa

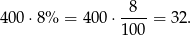
400 ⋅8% = 400 ⋅--8- = 32 . 1 00

Sposób II

Korzystając ze wzoru

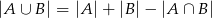
|A ∪ B | = |A |+ |B |− |A ∩ B|

Obliczamy ile procent uczniów uczy się języków

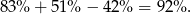
83% + 51% − 42% = 92 %.

W takim razie liczba uczniów, którzy nie uczą się żadnego języka jest równa

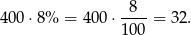
--8- 400 ⋅8% = 400 ⋅1 00 = 32 .

 
Odpowiedź: D

Wersja PDF