Zadanie nr 8951668
Rozwiązaniem nierówności 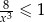 jest zbiór
jest zbiór
A) 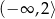 B)
B) 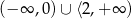 C)
C) 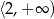 D)
D) 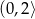
Rozwiązanie
Ze względu na mianownik musi być oczywiście 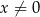 . Rozwiązujemy daną nierówność
. Rozwiązujemy daną nierówność
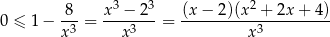
Trójmian kwadratowy w liczniku jest zawsze dodatni, więc powyższa nierówność jest równoważna nierówności
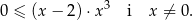
Rozwiązaniem tej nierówności jest zbiór
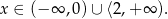
Odpowiedź: B

