Zadanie nr 9052058
Wskaż parę równań równoważnych
A) 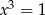 i
i 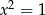 B)
B) 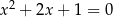 i
i 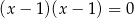
C) 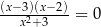 i
i 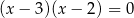 D)
D) 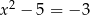 i
i 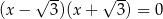
Rozwiązanie
Równania 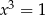 i
i 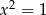 nie są równoważne, bo drugie jest spełnione przez
nie są równoważne, bo drugie jest spełnione przez 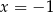 , a pierwsze nie.
, a pierwsze nie.
Równania 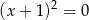 i
i 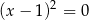 nie są równoważne, bo pierwiastkiem pierwszego jest
nie są równoważne, bo pierwiastkiem pierwszego jest 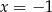 , a pierwiastkiem drugiego jest
, a pierwiastkiem drugiego jest 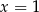 .
.
Równania 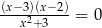 i
i 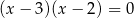 są równoważne, bo rozwiązaniem każdego z nich jest
są równoważne, bo rozwiązaniem każdego z nich jest 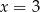 i
i 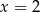 .
.
Równania 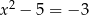 i
i 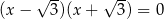 nie są równoważne, bo pierwsze możemy zapisać w postaci
nie są równoważne, bo pierwsze możemy zapisać w postaci 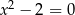 , a drugie w postaci
, a drugie w postaci 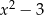 =0.
=0.
Odpowiedź: C

