/Szkoła średnia/Zadania testowe

Zadanie nr 9063687

Dodaj do ulubionych
Dodaj do rozwiązanych

W konkursie matematycznym, w którym przewidziano tylko jedną nagrodę I stopnia, bierze udział 15 uczniów. Prawdopodobieństwo, że zwycięży Agnieszka jest równe 0,20. Prawdopodobieństwo, że zwycięży Piotrek jest równe 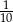-1 10 . Prawdopodobieństwo, że zwycięży Agnieszka lub Piotrek jest równe
A) 0,02 B) 0,3 C) 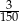-3- 150 D) 135

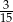
Rozwiązanie

Sposób I

Ponieważ może być tylko jeden zwycięzca zawodów, zdarzenia polegające na zwycięstwie Agnieszki i Piotrka są rozłączne (nie mogą zajść jednocześnie). W takim razie, prawdopodobieństwo, że zwycięży Agnieszka lub Piotrek jest równe

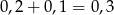
0,2 + 0,1 = 0,3

Sposób II

Niech 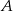A oznacza zdarzenie polegające na tym, że wygrywa Agnieszka, a 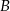B , że wygrywa Piotrek. Zwycięzca może być tylko jeden, więc 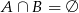A ∩ B = ∅ . Wówczas

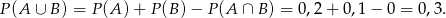
P (A ∪ B ) = P(A ) + P (B)− P(A ∩ B) = 0,2 + 0,1 − 0 = 0,3.

 
Odpowiedź: B

Wersja PDF