Zadanie nr 9089160
Bok 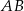 trójkąta
trójkąta 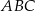 jest średnicą okręgu o środku
jest średnicą okręgu o środku 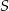 , a boki
, a boki 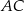 i
i 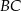 przecinają ten okrąg odpowiednio w punktach
przecinają ten okrąg odpowiednio w punktach 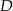 i
i 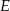 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 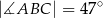 i
i 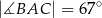 .
.
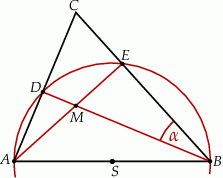
Zaznaczony na rysunku kąt  jest równy
jest równy
A) 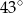 B)
B) 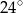 C)
C) 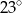 D)
D) 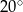
Rozwiązanie
Zauważmy, że kąty 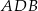 i
i 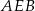 są oparte na średnicy
są oparte na średnicy 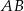 okręgu, więc oba są proste (czyli
okręgu, więc oba są proste (czyli 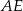 i
i 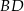 są wysokościami trójkąta
są wysokościami trójkąta 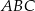 ).
).
Sposób I
Wiemy, że
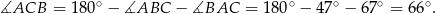
Zatem w trójkącie prostokątnym 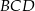 .
.
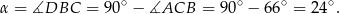
Sposób II
W trójkącie prostokątnym  mamy
mamy
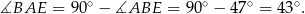
Stąd
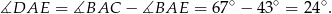
Teraz wystarczy zauważyć, że kąty 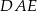 i
i 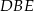 są oparte na tym samym łuku, więc
są oparte na tym samym łuku, więc
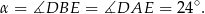
Sposób III
Tak jak w poprzednim sposobie zauważamy, że 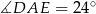 . Teraz wystarczy zauważyć, że trójkąty prostokątne
. Teraz wystarczy zauważyć, że trójkąty prostokątne 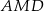 i
i 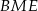 są podobne (bo mają wspólny kąt ostry przy wierzchołku
są podobne (bo mają wspólny kąt ostry przy wierzchołku 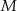 ). Zatem
). Zatem
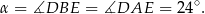
Odpowiedź: B

