/Szkoła średnia/Zadania testowe

Zadanie nr 9281723

Dodaj do ulubionych
Dodaj do rozwiązanych

W rozwinięciu wyrażenia 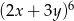6 (2x + 3y) współczynnik przy iloczynie 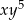5 xy jest równy
A) 1458 B) 2916 C) 972 D) 486

Rozwiązanie

Sposób I

Korzystamy ze wzoru

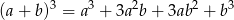
(a+ b)3 = a3 + 3a2b + 3ab2 + b3

na sześcian sumy. Mamy zatem

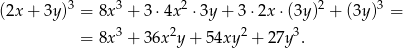
(2x + 3y)3 = 8x3 + 3 ⋅4x2 ⋅3y + 3 ⋅2x ⋅(3y)2 + (3y)3 = = 8x3 + 36x 2y+ 54xy2 + 27y 3.

W takim razie

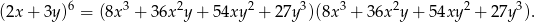
(2x + 3y )6 = (8x3 + 36x 2y+ 54xy2 + 27y 3)(8x 3 + 36x2y + 54xy 2 + 27y3).

Oczywiście nie musimy tych wyrażeń wymnażać, bo interesuje nas tylko współczynnik przy 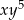xy 5 . Tego typu składnik otrzymamy w powyższym iloczynie na dwa sposoby:

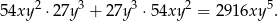
54xy 2 ⋅27y 3 + 2 7y3 ⋅ 54xy2 = 2 916xy5.

Sposób II

Korzystamy ze wzoru dwumianowego Newtona

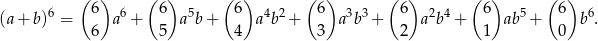
( ) ( ) ( ) ( ) ( ) ( ) ( ) 6 6 6 6 5 6 4 2 6 3 3 6 2 4 6 5 6 6 (a+ b ) = 6 a + 5 a b+ 4 a b + 3 a b + 2 a b + 1 ab + 0 b .

Nas interesuje współczynnik przy 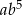5 ab , czyli składnik

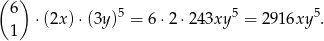
( ) 6 ⋅(2x) ⋅(3y)5 = 6 ⋅2 ⋅243xy 5 = 2916xy 5. 1

 
Odpowiedź: B

Wersja PDF