Zadanie nr 9394261
Wierzchołek paraboli będącej wykresem funkcji 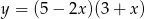 ma współrzędne
ma współrzędne
A) 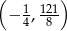 B)
B) 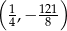 C)
C) 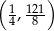 D)
D) 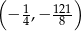
Rozwiązanie
Sposób I
Z podanego wzoru widać, że pierwiastkami danej funkcji są 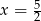 i
i 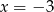 . Fakt istnienia pierwiastków oraz to, że ramiona paraboli są skierowane na dół oznacza, że jej wierzchołek musi być powyżej osi
. Fakt istnienia pierwiastków oraz to, że ramiona paraboli są skierowane na dół oznacza, że jej wierzchołek musi być powyżej osi 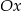 . To oznacza, że ma on współrzędne
. To oznacza, że ma on współrzędne 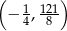 lub
lub 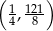 . Aby wyeliminować drugą możliwość wystarczy zauważyć, że wierzchołek musi być dokładnie w środku między pierwiastkami, czyli na lewo od osi
. Aby wyeliminować drugą możliwość wystarczy zauważyć, że wierzchołek musi być dokładnie w środku między pierwiastkami, czyli na lewo od osi  (bo -3 jest dalej od 0 niż 2,5).
(bo -3 jest dalej od 0 niż 2,5).
Sposób II
Korzystamy ze wzoru
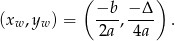
Wzór danej funkcji możemy zapisać w postaci
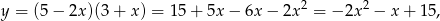
czyli
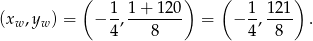
Sposób III
Jeżeli znamy miejsca zerowe 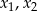 paraboli, to współrzędne wierzchołka możemy wyliczyć ze wzoru
paraboli, to współrzędne wierzchołka możemy wyliczyć ze wzoru
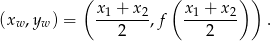
Wzór danej paraboli możemy zapisać w postaci
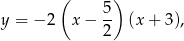
więc jej miejsca zerowe to 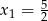 i
i 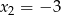 . Zatem
. Zatem
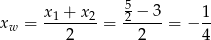
oraz
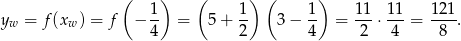
Odpowiedź: A

