/Szkoła średnia/Zadania testowe

Zadanie nr 9423609

Dodaj do ulubionych
Dodaj do rozwiązanych

W ciągu geometrycznym 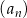(an) , określonym dla 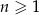n ≥ 1 , wszystkie wyrazy są niezerowe, oraz iloczyn 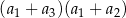(a1 + a3)(a1 + a2) jest trzy razy mniejszy od pierwszego wyrazu tego ciągu. Suma czterech początkowych wyrazów ciągu 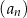(an) jest równa
A) 3 B) 1 C) 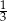1 3 D) 9

Rozwiązanie

Próbujemy rozszyfrować podaną informację

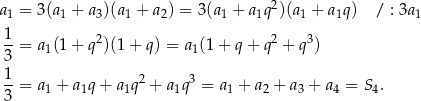
2 a1 = 3(a1 + a3)(a1 + a2) = 3(a1 + a1q )(a1 + a1q) / : 3a1 1- 2 2 3 3 = a1(1 + q )(1 + q) = a1(1 + q + q + q ) 1 --= a1 + a1q + a1q2 + a1q3 = a1 + a2 + a3 + a4 = S4. 3

 
Odpowiedź: C

Wersja PDF