Zadanie nr 9554517
Z pudełka zawierającego dwa rodzaje monet wybieramy losowo dwie. Prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej jest równe 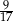 , a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe 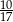 . Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
. Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
A) 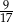 B)
B) 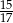 C)
C) 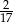 D)
D) 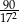
Rozwiązanie
Jeżeli 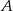 oznacza prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej, a
oznacza prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej, a 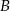 prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej, to
prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej, to
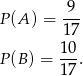
Ponadto 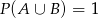 (bo zawsze wylosujemy co najmniej jedną monetę dwu lub pięciozłotową) oraz szukane przez nas prawdopodobieństwo to
(bo zawsze wylosujemy co najmniej jedną monetę dwu lub pięciozłotową) oraz szukane przez nas prawdopodobieństwo to 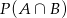 (bo jak ma być dokładnie jedna moneta dwuzłotowa, to druga musi być pięciozłotowa). Mamy więc
(bo jak ma być dokładnie jedna moneta dwuzłotowa, to druga musi być pięciozłotowa). Mamy więc
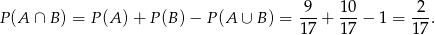
Odpowiedź: C

