Zadanie nr 9565417
Ze zbioru liczb 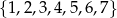 losujemy kolejno dwa razy po jednej cyfrze bez zwracania. Zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Prawdopodobieństwo otrzymania liczby większej od 32 jest równe
losujemy kolejno dwa razy po jednej cyfrze bez zwracania. Zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Prawdopodobieństwo otrzymania liczby większej od 32 jest równe
A) 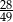 B)
B) 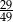 C)
C) 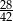 D)
D) 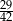
Rozwiązanie
Obliczamy liczbę wszystkich zdarzeń
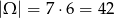
(pierwszą cyfrę możemy wybrać na 7, a drugą na 6 sposobów).
Obliczmy teraz, ile jest zdarzeń sprzyjających. Jeżeli pierwszą z wylosowanych cyfr jest 3, to druga cyfra musi być równa: 4, 5, 6 lub 7. Są więc 4 zdarzenia tego typu. Jeżeli natomiast pierwsza cyfra jest jedną z cyfr: 4, 5, 6, 7, to druga cyfra jest dowolna, więc są
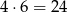
zdarzenia tego typu. Prawdopodobieństwo jest więc równe
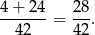
Odpowiedź: C

