/Szkoła średnia/Zadania testowe

Zadanie nr 9572047

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja wykładnicza określona wzorem 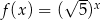√ -- x f(x) = ( 5 ) przyjmuje wartość 2 dla argumentu
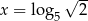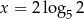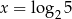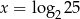
A) √ -- x = log 2 5 B) x = 2log 2 5 C) x = log 5 2 D) x = log 25 2

Rozwiązanie

Szukamy takiej liczby x , dla której

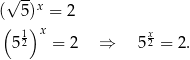
√ --x (( 5)) = 2 12 x x2 5 = 2 ⇒ 5 = 2 .

Sposób I

Z definicji logarytmu mamy

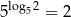
log 2 5 5 = 2

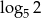(log52 to liczba do jakiej należy podnieść 5, żeby otrzymać 2). Zatem

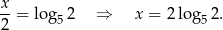
x- 2 = log 52 ⇒ x = 2log5 2.

Sposób II

Musimy rozwiązać równanie

x 52 = 2

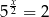
Logarytmujemy tę równość stronami logarytmem przy podstawie 5 i mamy

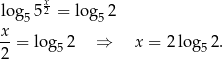
x log55 2 = log5 2 x --= log 52 ⇒ x = 2log5 2. 2

Sposób III

Obie strony równości

√ -- ( 5)x = 2

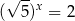
są dodatnie, więc możemy podnieść tę równość stronami do kwadratu.

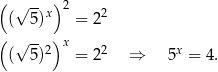
( √ -- )2 ( 5)x = 22 ( ) √ --2 x 2 x ( 5) = 2 ⇒ 5 = 4.

Równość tę spełnia liczba

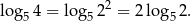
lo g54 = lo g522 = 2 log52 .

 
Odpowiedź: B

Wersja PDF