/Szkoła średnia/Zadania testowe

Zadanie nr 9588721

Dodaj do ulubionych
Dodaj do rozwiązanych

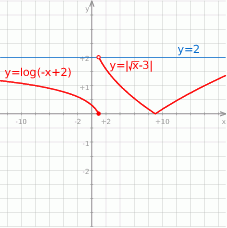
Dana jest funkcja 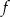f określona wzorem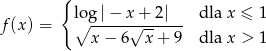 { f(x) = l∘og-|−--x√+--2|-- dla x ≤ 1 x − 6 x + 9 dla x > 1
Równanie 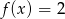f(x ) = 2 ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) trzy rozwiązania. D) cztery rozwiązania.

Rozwiązanie

Zauważmy, że

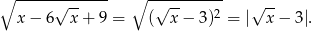
∘ -----√------- ∘ -√--------- √ -- x − 6 x + 9 = ( x − 3)2 = | x − 3|.

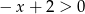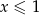Ponadto − x+ 2 > 0 dla x ≤ 1 , więc daną funkcję możemy zapisać w postaci

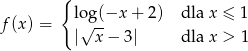
{ f(x) = lo√g(−x + 2) dla x ≤ 1 | x− 3| dla x > 1

Rozwiązujemy najpierw równanie

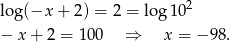
log (−x + 2 ) = 2 = log 102 − x+ 2 = 100 ⇒ x = − 98.

Liczba ta oczywiście spełnia warunek 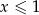x ≤ 1 .

Teraz rozwiązujemy drugie równanie

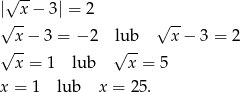
√ -- | x − 3| = 2 √x-− 3 = − 2 lub √x--− 3 = 2 √ -- √ -- x = 1 lub x = 5 x = 1 lub x = 2 5.

Tylko druga z tych liczb spełnia warunek 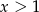x > 1 .

Równanie 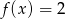f (x) = 2 ma więc dwa rozwiązania.

PIC

 
Odpowiedź: B

Wersja PDF