/Szkoła średnia/Zadania testowe

Zadanie nr 9627235

Dodaj do ulubionych
Dodaj do rozwiązanych

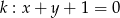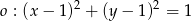Ile punktów wspólnych ma prosta k : x+ y+ 1 = 0 z okręgiem o : (x − 1)2 + (y − 1)2 = 1 ?
A) 3 B) 2 C) 1 D) 0

Rozwiązanie

Sposób I

Z równania prostej wyznaczamy

y = −x − 1

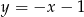
i podstawiamy to wyrażenie do równania okręgu.

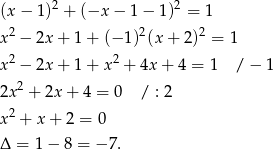
2 2 (x − 1) + (−x − 1 − 1) = 1 x2 − 2x + 1 + (− 1)2(x + 2 )2 = 1 x2 − 2x + 1 + x 2 + 4x + 4 = 1 / − 1 2 2x + 2x + 4 = 0 / : 2 x2 + x + 2 = 0 Δ = 1 − 8 = − 7.

Ponieważ wyróżnik jest ujemny, równanie nie ma rozwiązań. Zatem prosta i okrąg nie mają punktów wspólnych.

Sposób II

Dany okrąg to okrąg o środku 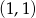(1,1) i promieniu 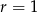r = 1 , a dana prosta 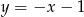y = −x − 1 to prosta 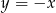y = −x przesunięta o jedną jednostkę w dół. Łatwo teraz wykonać szkicowy rysunek.

PIC

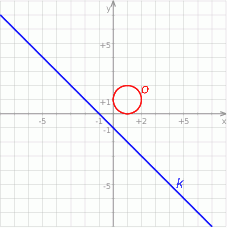
Z obrazka widać, że prosta i okrąg są rozłączne.  
Odpowiedź: D

Wersja PDF