Zadanie nr 9656227
Wierzchołek paraboli 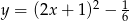 leży na prostej o równaniu
leży na prostej o równaniu
A) 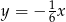 B)
B) 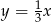 C)
C) 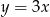 D)
D) 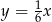
Rozwiązanie
Sposób I
Przypomnijmy, że postacią kanoniczną funkcji kwadratowej jest
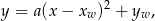
gdzie 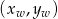 są współrzędnymi wierzchołka. Zatem podany wzór nie jest postacią kanoniczną, ale łatwo go do niej sprowadzić.
są współrzędnymi wierzchołka. Zatem podany wzór nie jest postacią kanoniczną, ale łatwo go do niej sprowadzić.
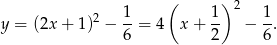
Wierzchołek ma więc współrzędne 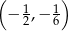 , które spełniają
, które spełniają 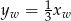 .
.
Sposób II
Możemy też znaleźć współrzędne wierzchołka ze wzoru
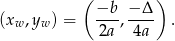
Liczymy
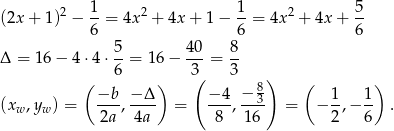
Jak poprzednio zauważamy, że 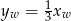 .
.
Odpowiedź: B

