/Szkoła średnia/Zadania testowe

Zadanie nr 9779126

Dodaj do ulubionych
Dodaj do rozwiązanych

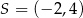Punkt S = (− 2,4 ) jest środkiem okręgu. Na okręgu leży punkt 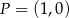P = (1,0) . Równanie tego okręgu ma postać
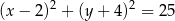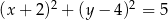
A) (x − 2)2 + (y + 4)2 = 2 5 B) (x + 2)2 + (y − 4)2 = 5
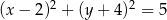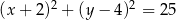
C) 2 2 (x − 2) + (y + 4) = 5 D) 2 2 (x + 2) + (y − 4) = 2 5

Rozwiązanie

Zaczynamy od rysunku

PIC

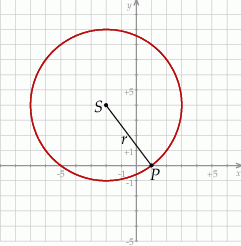
Przypomnijmy, że równanie okręgu o środku w punkcie 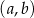(a,b) i promieniu r to

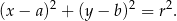
(x− a)2 + (y− b)2 = r2.

Obliczamy długość promienia

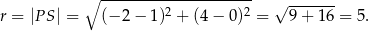
∘ --------------------- r = |P S| = (− 2 − 1)2 + (4 − 0)2 = √ 9-+-16-= 5.

Zatem okrąg jest dany wzorem

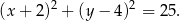
2 2 (x + 2) + (y − 4) = 25.

 
Odpowiedź: D

Wersja PDF