Zadanie nr 9784570
Dany jest okrąg o środku w punkcie 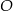 . Prosta
. Prosta 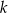 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 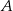 .
.
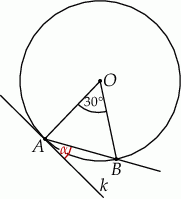
Miara kąta 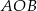 wynosi
wynosi 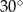 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 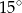 B)
B) 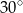 C)
C) 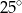 D)
D) 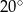
Rozwiązanie
Sposób I
Boki 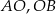 są promieniami okręgu, więc trójkąt
są promieniami okręgu, więc trójkąt 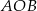 jest równoramienny. Zatem
jest równoramienny. Zatem
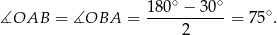
Teraz wystarczy zauważyć, że styczna  jest prostopadła do promienia
jest prostopadła do promienia  , więc
, więc
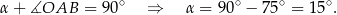
Sposób II
Dorysujmy kąt wpisany 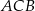 .
.
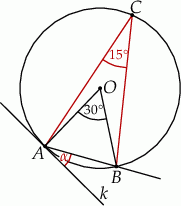
Na mocy twierdzenia o kątach wpisanym i środkowym opartych na tym samym łuku, mamy 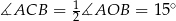 . Teraz wystarczy skorzystać z twierdzenia o stycznej:
. Teraz wystarczy skorzystać z twierdzenia o stycznej:
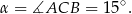
Odpowiedź: A

