/Szkoła średnia/Zadania testowe

Zadanie nr 9836526

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 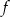f określona wzorem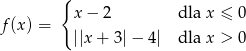 { f(x) = x− 2 dla x ≤ 0 ||x + 3|− 4| dla x > 0
Równanie 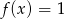f(x ) = 1 ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) cztery rozwiązania. D) pięć rozwiązań.

Rozwiązanie

Sposób I

Rozwiązujemy najpierw równanie

x − 2 = 1 ⇒ x = 3

Liczba ta nie spełnia jednak nierówności 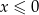x ≤ 0 , więc w tym przypadku równanie nie ma rozwiązań.

Rozwiązujemy teraz drugie równanie

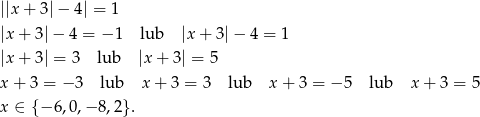
||x+ 3|− 4| = 1 |x + 3|− 4 = − 1 lub |x+ 3|− 4 = 1 |x + 3| = 3 lub |x+ 3| = 5 x + 3 = −3 lub x+ 3 = 3 lub x + 3 = − 5 lub x + 3 = 5 x ∈ { − 6,0,− 8,2}.

Tylko 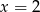x = 2 spełnia nierówność 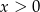x > 0 , więc jest to jedyne rozwiązanie równania f (x) = 1 .

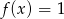Sposób II

Zauważmy, że jeżeli 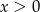x > 0 , to

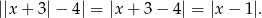
||x + 3 |− 4| = |x + 3− 4| = |x− 1|.

Zatem wzór funkcji możemy zapisać w postaci

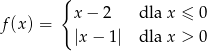
{ x− 2 dla x ≤ 0 f(x) = |x − 1 | dla x > 0

Dokładnie tak samo jak w poprzednim sposobie stwierdzamy, że równanie 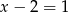x − 2 = 1 jest sprzeczne, więc pozostaje równanie

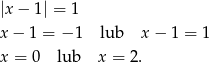
|x − 1| = 1 x− 1 = − 1 lub x − 1 = 1 x = 0 lub x = 2 .

Tylko druga z tych liczb spełnia warunek 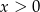x > 0 .

Sposób III

Tak samo jak w poprzednim sposobie stwierdzamy, że

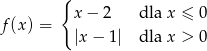
{ f(x) = x− 2 dla x ≤ 0 |x − 1 | dla x > 0

Szkicujemy teraz wykres funkcji 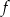f .

PIC

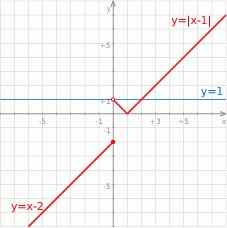
Z wykresu widać, że równanie 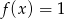f (x) = 1 ma dokładnie jedno rozwiązanie.  
Odpowiedź: A

Wersja PDF